
Salut la communauté
On se retrouve aujourd'hui pour un petit cours d'Informatique

Un bon nombre d'entre vous sont en spécialité ISN au lycée où sont peut-être simplement curieux...
Ce tutoriel est simple et n'importe qui pourra le comprendre (oui, même toi, le L
 )
)Voici donc un tutoriel simple sur les conversions entre binaire, décimal et hexadécimal !

Introduction
Pour commencer il va falloir vous définir ces 3 mots que sont binaire, décimal et hexadécimal.
Ces 3 mots font partie de ce qu'on appelle les systèmes de numération.
Il existe une infinité de systèmes de numération, ici nous allons en étudier les plus utilisés en informatique.
Remarque: Le binaire s'écrit sous forme d'octet, ici, nous négligerons cette écriture.
Je vais ici vous présenter 5 méthodes de conversion:
- Du binaire au décimal
- Du décimal au binaire
- De l'hexadécimal au binaire
- De l'hexadécimal au décimal
- Du décimal à l'hexadécimal

Binaire
Pour vous aider à comprendre, je vais d'abord vous parler du binaire.
Le binaire est un système de numération qu'on qualifie de « base 2 ».
Cela signifie tout simplement qu'on ne peut écrire le binaire qu'avec 2 caractères différents.
En informatique, le binaire est composé de 2 caractères qui sont le 0 et le 1.
Vous pouvez écrire des mots grâce au binaire, mais ici nous n'allons nous intéresser qu'à des chiffres !
Exemple: En binaire, écrire « 0010 » se traduit par « 2 ».
Remarque: Votre ordinateur fonctionne grâce au binaire.
Remarque 2: On regroupe le binaire par groupe de 4 (00100010 = 0010 0010).

Décimal
Le décimal est un système de numération qu'on qualifie de « base 10 ».
Encore une fois, rien de sorcier, on l'écrit avec 10 caractères différents.
Exemple: En décimal, écrire « 255 » se traduit par « 255 ».
Remarque: C'est le système de numérotation que l'on utilise tous les jours !

Hexadécimal
Pour l'hexadécimal, on a donc un système de numération qu'on qualifie de « base 16 ».
Et on écrit l'hexadécimal avec... 16 caractères différents ! (bravo...)
En informatique, on se sert des chiffres, mais l'hexadécimal est un système de numération particulier...
Pour le décimal, rien de sorcier, on se sert des chiffres allant de 0 à 9 (0, 1, ..., 9).
Cependant, par principe, on se sert uniquement de chiffres, et donc pas de nombre !
Comment on fait pour l'hexadécimal s'il y a 16 caractères différents et qu'on ne va pas au-dessus de 9 ?!
On va cette fois-ci utiliser, exceptionnellement, des lettres !
L’hexadécimal va donc de 0 à 9 et de A à F (A = 10, B = 11, ..., F= 15) !
Exemple: En hexadécimal, écrire « 9E » se traduit par « 158 ».
Remarque: C'est le système utilisé par les codeurs pour les couleurs sur le web.

Du Binaire au Décimal
Nous allons ici utiliser un principe pour les conversions qui utilisent le binaire: les puissances de 2.
Pourquoi ? Car le binaire est en base 2, donc on se sert des puissances de 2 !
Pour comprendre, on va commencer par des nombres simples. Allons de 2⁰ à 2⁵.
Dans le tableau ci-dessous, j'ai simplement remplacé les 2⁰ à 2⁵ par leurs résultats. (2⁰ = 1 et à 2⁵ = 32).

Admettons que l'on nous donne l'écriture binaire suivante: 00 11010.
Pour traduire cette écriture en base 2, on rentre cette écriture dans le tableau.
Il nous suffit ensuite de se servir des cases où on retrouve des 1 pour calculer le résultat par somme !

Les cases en 1 sont: 16, 8 et 2. On a donc 16+8+2 = 26 !
Ainsi, 00 11010 en base 2 vaut 26 en décimal !
Remarque: 0011010 ne vaut 26 qu'en conversion décimale. Vous comprendrez pourquoi plus tard.
Prenons deux autres exemples: 010 et 1110 0010.
010 n'a pas assez de chiffres tandis que 1110 0010 en a trop... Peu importe !
Il suffit de remplir les cases comme si de rien était pour 010 et d'en rajouter jusqu'à 2⁷ pour 1110 0010 !

On a donc 010 = 2 et 1110 0010 = 128+64+32+1 = 225 !
Remarque: 010 peut être écrit 0000 0010 ou encore 0000 0000 0010.

Du Décimal au Binaire
Nous allons ici utiliser une nouvelle fois le principe des puissances de 2 !
Nous allons nous intéresser ici aux nombres allant jusqu'à 255 uniquement (et donc un tableau jusqu'à 2⁷).
Cette fois-ci on part du nombre que l'on cherche à deviner et on doit procéder de la manière suivante:
Est-ce que je peux soustraire mon nombre par celui-là pour obtenir mon nombre à la fin ?
Exemple avec 8:
Est-ce que je peux soustraire 8 par 128 pour obtenir 8 à la fin ? NON
Est-ce que je peux soustraire 8 par 64 pour obtenir 8 à la fin ? NON
[...]
Est-ce que je peux soustraire 8 par 8 pour obtenir 8 à la fin ? OUI
Or si je soustrais 8 à 8, j'obtiens 0. Donc on s'arrête à 8.
On commence au premier nombre qu'on peut soustraire et on vérifie:
Est-ce que je peux soustraire 8 par 8 pour obtenir 8 à la fin ? OUI (8-8 = 0)
Est-ce que je peux soustraire 8 par 4 pour obtenir 8 à la fin ? NON (8-8-4 = -4)
Est-ce que je peux soustraire 8 par 2 pour obtenir 8 à la fin ? NON (8-8-2 = -2)
Est-ce que je peux soustraire 8 par 1 pour obtenir 8 à la fin ? NON (8-8-1 = -1)
8 en base 2 (binaire) est donc 0000 1000 (ou 1000) !
Est-ce que je peux soustraire 8 par 64 pour obtenir 8 à la fin ? NON
[...]
Est-ce que je peux soustraire 8 par 8 pour obtenir 8 à la fin ? OUI
Or si je soustrais 8 à 8, j'obtiens 0. Donc on s'arrête à 8.
On commence au premier nombre qu'on peut soustraire et on vérifie:
Est-ce que je peux soustraire 8 par 8 pour obtenir 8 à la fin ? OUI (8-8 = 0)
Est-ce que je peux soustraire 8 par 4 pour obtenir 8 à la fin ? NON (8-8-4 = -4)
Est-ce que je peux soustraire 8 par 2 pour obtenir 8 à la fin ? NON (8-8-2 = -2)
Est-ce que je peux soustraire 8 par 1 pour obtenir 8 à la fin ? NON (8-8-1 = -1)
8 en base 2 (binaire) est donc 0000 1000 (ou 1000) !
Exemple avec 163:
Est-ce que je peux soustraire 163 par 128 pour obtenir 163 à la fin ? OUI
Est-ce que je peux soustraire 163 par 64 pour obtenir 163 à la fin ? OUI
Est-ce que je peux soustraire 163 par 32 pour obtenir 163 à la fin ? OUI
Est-ce que je peux soustraire 163 par 16 pour obtenir 163 à la fin ? OUI
Est-ce que je peux soustraire 163 par 8 pour obtenir 163 à la fin ? OUI
Est-ce que je peux soustraire 163 par 4 pour obtenir 163 à la fin ? OUI
Est-ce que je peux soustraire 163 par 2 pour obtenir 163 à la fin ? OUI
Est-ce que je peux soustraire 163 par 1 pour obtenir 163 à la fin ? OUI
Ce cas de figure est un peu plus complexe que le précédent
On va donc chercher à soustraire 163 jusqu'à obtenir un résultat de 0 !pas plus, pas moins) !
On commence avec le premier nombre qu'on peut soustraire.
On note 1 si on peut soustraire, 0 si on ne peut pas...
1 163-128 = 35.
0 Or, 35-64 < 0 donc on ne peut pas soustraire par 64.
1 Cependant, 35-32 = 3.
0 Or, 3-16 < 0
0 3-8 < 0
0 3-4 < 0
1 Cependant, 3-2 = 1
1 Et 1-1 = 0
On a donc: 1010 0011
163 en base 2 (binaire) est donc 1010 0011 !
Est-ce que je peux soustraire 163 par 64 pour obtenir 163 à la fin ? OUI
Est-ce que je peux soustraire 163 par 32 pour obtenir 163 à la fin ? OUI
Est-ce que je peux soustraire 163 par 16 pour obtenir 163 à la fin ? OUI
Est-ce que je peux soustraire 163 par 8 pour obtenir 163 à la fin ? OUI
Est-ce que je peux soustraire 163 par 4 pour obtenir 163 à la fin ? OUI
Est-ce que je peux soustraire 163 par 2 pour obtenir 163 à la fin ? OUI
Est-ce que je peux soustraire 163 par 1 pour obtenir 163 à la fin ? OUI
Ce cas de figure est un peu plus complexe que le précédent
On va donc chercher à soustraire 163 jusqu'à obtenir un résultat de 0 !pas plus, pas moins) !
On commence avec le premier nombre qu'on peut soustraire.
On note 1 si on peut soustraire, 0 si on ne peut pas...
1 163-128 = 35.
0 Or, 35-64 < 0 donc on ne peut pas soustraire par 64.
1 Cependant, 35-32 = 3.
0 Or, 3-16 < 0
0 3-8 < 0
0 3-4 < 0
1 Cependant, 3-2 = 1
1 Et 1-1 = 0
On a donc: 1010 0011
163 en base 2 (binaire) est donc 1010 0011 !
Voici un tableau d'exemple avec d'autres nombres. Faites bien attention: le résultat final doit être 0.

Cette notion semble complexe à comprendre à priori mais elle est vraiment très simple, concentrez-vous bien !

Hexadécimal au Binaire
Nous allons ici utiliser une nouvelle fois le principe des puissances de 2 ! (à chaque fois qu'on aura du binaire !)
Contrairement à précédemment, je vous explique seulement comment passer du hexadécimal au binaire...
Vous vous dites sans doute que je suis un flemmard paresseux mais... non, il y a une raison à cela !
C'est tout simplement car le secret de cette conversion... est un tableau à double lecture !
Voici le tableau qui correspond à la conversion hexadécimal/binaire:
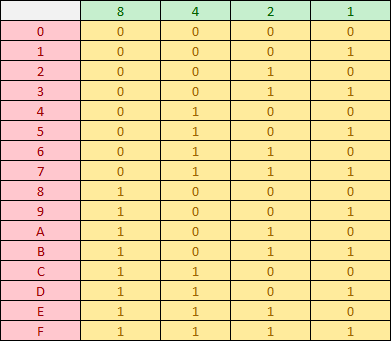
Pour comprendre ce tableau, voici une légende:
Vert: Puissances de 2
Rouge: Hexadécimal (0 à 9 et A à F)
Jaune: Résultat en binaire
Pour comprendre ce tableau, vous devez vous rappeler que A = 10, B = 11, ..., F = 15.
En fait, le principe marche comme pour la conversion du décimal au binaire.
Cependant, nous allons plus loin car cette fois-ci nous avons 16 caractères !
Pour trouver la valeur de D en binaire par exemple, c'est simple:
On sait que D = 13. Pour obtenir 13 en binaire il faut faire 8+4+1 d'après les nombres du tableau donc D = 1101 !
Remarque: On peut dégager une logique et retrouver les binaires facilement.
Nous avons donc les résultats suivants:
0 = 0000
1 = 0001
2 = 0010
3 = 0011
4 = 0100
5 = 0101
6 = 0110
7 = 0111
8 = 1000
9 = 1001
A = 1010
B = 1011
C = 1100
D = 1101
E = 1110
F = 1111
1 = 0001
2 = 0010
3 = 0011
4 = 0100
5 = 0101
6 = 0110
7 = 0111
8 = 1000
9 = 1001
A = 1010
B = 1011
C = 1100
D = 1101
E = 1110
F = 1111

Hexadécimal au Décimal
Laissons un peu tomber les puissances de 2 ! Nous sommes des pro du calcul !
On va maintenant calculer du hexadécimal, donc passons à la base 16 !
Mais non ! Ne partez pas ! Ce n'est pas compliqué vous allez voir

On va donc s'occuper des puissances de 16...
Mais ne prenez pas peur, nous allons nous servir de 16⁰ et 16¹ uniquement ! (olala c'est dur...)
Prenons par exemple un code couleur symbolisant du orange.
Prenons la couleur orange que j'utilise pendant mes rédactions: #FF8000 !
On va séparer ce code couleur en trois parties: Rouge, vert, bleu (RGB pour les connaisseurs...).
On obtient FF, 80 et 00.
On va donc convertir ces codes séparément.
Il va falloir se servir donc des 16⁰ et 16¹ dont on parlait tout à l'heure...
On sait que F = 15 en hexadécimal. Or on a FF.
Cette fois-ci, on doit faire un opération avec x = le premier caractère et y = le deuxième caractère:
16¹*x + 16⁰*y
On a donc 16*15 + 15 = 255 ; 16*8 + 0 = 128 ; 16*0 + 0 = 0 !
Si on refait un tableau similaire à précédemment on obtient:
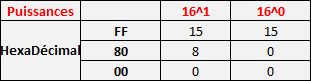
Rien de compliqué donc... Et on obtient en RGB:
RGB(255,128,0)
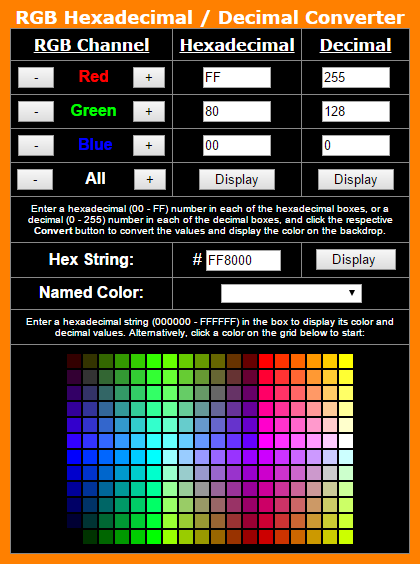
Et vous pouvez vérifier votre code à tout moment sur le site
Vous devez être inscrit pour voir les liens ! Inscrivez-vous ou connectez-vous ici.
Vous devez être inscrit pour voir les liens ! Inscrivez-vous ou connectez-vous ici.
Et évidemment, vous ne trouverez aucun problème


Décimal à l'Hexadécimal
Pour passer du décimal à l'hexadécimal, c'est assez particuliers...
Il y a plusieurs méthodes mais je vais vous présenter celle que j'utilise.
Le but va être de faire ça en 2 étapes... que vous connaissez déjà !
Première étape: Passer du décimal au binaire.
Deuxième étape: Passer du binaire à l'hexadécimal !
Par exemple avec le nombre 158.
Première étape: 158 en décimal => 1001 1110 en binaire.
Deuxième étape: 1001 1110 en binaire => 9E en hexadécimal.
Ce sont des étapes que vous connaissez, alors rien de compliqué !
Exemple d'un tableau avec la couleur verte: RGB(158,212,56):
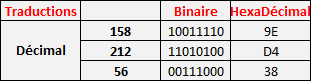
On aurait donc #9ED438 en hexa !

Et le plus beau dans l'histoire ? C'est terminé !
Je n'ai plus rien à vous apprendre sur ces 3 systèmes de numérotation !
J'espère que ce tutoriel vous aura plu, il m'aura prit du temps à la rédaction
À bientôt


 Je ferai des recherches dessus, merci
Je ferai des recherches dessus, merci 


